CUET-General Aptitude-06/05/2025
Dear Students, we welcome you in our post CUET-General Aptitude-06/05/2025.
In all previous years’ exams, there is at least one question on ‘algebraic expressions’.
Today’s post will demonstrate how to solve questions on algebraic expressions:
Q 3700) If p=0, the value of p(p² +p +1) +5 would be
Ans: 5
Solution: (0)3 + (0)² + (0) +5 = 5
Q 3701) The sum of
-3zx
+9zx -4y
-3zx +5x is
Ans: +3zx +5x -4y
Q 3702) The subtract -4y² +6y -3 from +8y² +5x -3y is
Ans: +12y² +5x -9y
Q 3703) If p=3, the value of 3p(4p -5) + 3 would be
Ans: 66
Solution: 12 (3)² -15(3) +3
=12×9 -15 x 3 +3
=108 -45 +3 =66
Q 3704) If p=1, the value of p(p² +p +1) +5 would be
Ans: 8
Solution: (1)3 + (1 )² + (1 ) +5
= 1 +1 +1 +5 = 8
Q 3705) If p=-1, the value of p(p² +p +1) +5 would be
Ans: 4
Solution: (-1)3 + (-1)² + (-1) +5
= -1 + 1 -1 + 5
= -1 + 5 =4
Q 3706) If p=0, the value of p(p² +p +1) +5 would be
Ans: 5
Solution: (0)3 + (0)² + (0) +5 = 5
Area of a triangle
Q 3707) In the given figure ΔPQR is isosceles with PQ = PR = 7.5 cm and QR = 9 cm. The height PS from P to QR is 6 cm, then the area of PQR is …
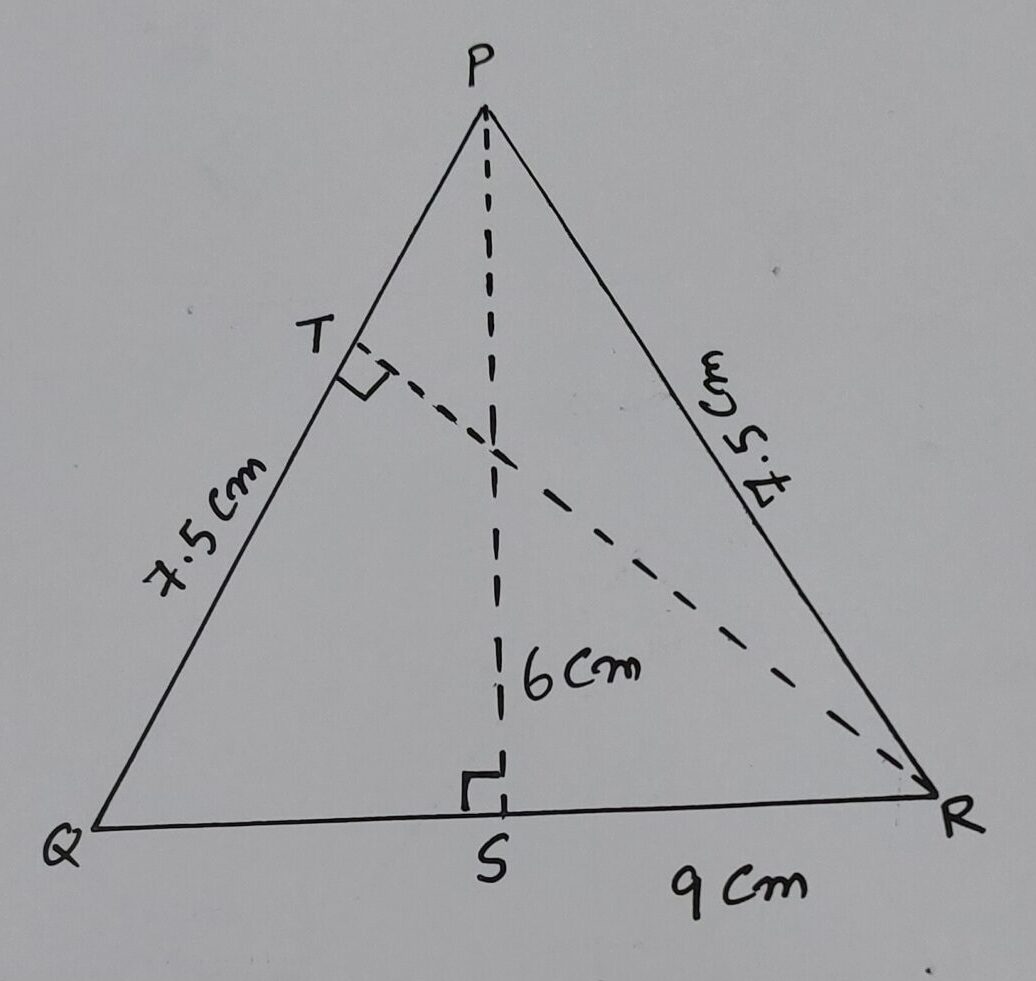
Ans: Area of ΔPQR is 27 cm²
Solution: Area of ΔPQR with base QR = 1/2 x base x height
= 1/2 x QR x PS = 1/2 x 9 x 6 = 27 cm²
Q 3708) In the given figure ΔPQR is isosceles with PQ = PR = 7.5 cm and QR = 9 cm. The height RT from R to PQ is …

Ans: 7.2 cm
Solution: Area of ΔPQR with base PQ = 1/2 x base x height = 1/2 x PQ x RT
27 cm² = 1 /2 x 7.5 cm x RT
RT = 27 cm² x 2 / 7.5 cm = 7.2 cm
Thank you for watching the post!
General Aptitude
This post ‘CUET2025-General Aptitude-06/05/2025’ is important for CUET (UG) General Aptitude Test Preparation.
इस वेबसाइट को हमनें बड़ी मेहनत से बनाया है। यह आपके लिए बिल्कुल निःशुल्क है। Pleasev Leave a comment box में अपने comment ज़रूर लिखेंI

That’s very good website for preparation of CUET.